空间与变换
大部分的计算机图形和计算机动画都包括空间变换数据。我们将对象数据从自定义的空间变换到世界空间,以便构建相应的虚拟环境。为了产生动画,对象数据是以时间为基准进行变换的。最后,对象数据的变换目的是在屏幕上浏览这个对象。图形学中使用4×4的变换矩阵来表达各种变换过程,这种矩阵表达方式可以表示三维旋转、平移和缩放操作的组合。
我们可以使用左手坐标系或者右手坐标系来定义一个坐标空间。

左手坐标系-Z轴指向纸张的内部 右手坐标系-z轴指向纸张的外部
左手坐标系的x、y和z坐标轴与左手的大拇指、食指和中指依次对齐,并且保持一个适当的角度,即大拇指向手外侧伸开,食指与手掌共面,中指与手掌垂直。右手坐标系采用类似的方式,通过右手来布置。这两者间存在根本的不同,因此我们无法通过单纯的旋转变换将左手坐标系的坐标转换到右手坐标系。至于我们该采用哪种定义方式,这就是转换时要考虑的问题了。事实上,对于我们来说,这两者在使用上并没有什么不一样。我们还需要考虑坐标轴的变换过程中对向上向量(up vector)的定义。有的应用程序假设y轴是“向上”的,其他的应用程序可能会假设z轴“向上”。无论对于左手坐标系还是右手坐标系,只要我们预先知道这种假设关系,那么变换就不会有本质的区别。
显示流水线
显示流水线指的是对象数据从原始定义的空间变换到一系列中间空间,并最终映射到屏幕上的过程。我们将对象数据变换到不同空间的目的是更高效地计算光照,根据可视范围对数据进行裁剪,以及执行透视变换操作。在本小节中,我们将回顾这些空间的定义、属性,以及数据从一个空间映射到下一个空间的变换过程,当然还有这些变换所需的参数。这些空间的命名方式在不同的资料里有所区别,因此有必要在这里将它们的命名统一起来。
裁剪(clipping)是一个重要的过程,它负责将那些可视范围之外的线或者一部分线消隐掉,但是由于它与运动控制并没有什么联系,因此我们不会在这里提及。
对象原始定义的空间又被称做对象空间(object space)。对象空间的数据通常位于原点,并且放置于某个标准的限制范围内,如-1到+1。对象是通过一系列数据点定义的(或者说是顶点,vertex),其变换过程通常包括一系列的旋转、平移和缩放,并最终变换到世界空间( world space),也就是观察者所见的整个世界环境(对象均放置于其中)。对象空间和世界空间一般都是右手坐标系的空间。
世界空间同时也是光源和观察者所处的空间。在本书中,我们认为观察者的位置(observer position)与摄像机位置(camera position;或者人眼位置,eye position)是同义的,并且可以相互替换。观察者的参数主要包括其位置和它的方位。其中方位是完全通过观察的方向(view direction)和向上向量(upvector)决定的。我们可以使用多种不同的方法来定义这些方位向量。有时我们需要用兴趣中心(centerof interest,COI)来设置观察的方向,此时观察方向指的是从观察者(或者人眼位置,EYE)出发到兴趣中心的向量。人眼位置也就是观察的起始点,而兴趣中心就是观察的目标点。默认的直视方位的定义为,观察者的向上向量与观察方向垂直,并且位于观察方向和全局y轴共同定义的平面内。
如果从当前的向上向量向外转动,那么就相当于观察者的头部发生了倾斜。
为了快速将数据投影到观察平面上,我们需要将数据定义到摄像机相关的坐标系,即以摄像机为中心的坐标系(u,v,w)。其中,v轴即观察者的y轴,或者向上向量,而w轴就是观察者的z轴。在本书中,我们假设摄像机使用左手坐标系。因此,其个向量在右手坐标系的世界空间中的计算方法为,首先计算观察方向向量和y轴的叉积,从而得到u向量,然后计算u向量与观察方向向量的叉积,如式2-1所示。
w=COI-EYE (view direction vector)
u=w×(0,1,0) ( cross produc withy-axis)
当计算得到这些向量之后,我们需要将它们归一化,以便获得一个位于眼睛位置的单位坐标系。之后世界空间的数据点就可以设法定义在这个坐标系内,如计算从眼睛到数据点的向量与3个坐标轴向量的点积。
头部倾斜的信息可以通过一种或两种方式给出。当给定沿竖直方向旋转的角度时,我们可以把一个头部倾斜的旋转矩阵叠加到世界一眼睛空间的变换当中,或者直接设置给观察者的默认u和v向量。
另一种处理头部倾斜信息的方式是直接指定一个向上方向向量。用户定义的向上方向向量通常不一定与观察方向垂直,否则对于用户而言工作量太大。对于用户给出的向量而言,它与当前的观察方向向量共同定义了一个平面,真正的向上向量必定在这个平面中。用户定义的向上方向向量与向上向量之间的区别是,后者必定与观察方向向量垂直。向上向量的计算方法与式左右手坐标系中所述相同,但是需要用用户定义的向上方向向量代替y轴。
w=COI-EYE ( view direction vector)
u=w×UP ( cross produc with user'supvector)
我们使用默认的向上向量时需要多加小心。由于它被定义为与观察方向垂直并且位于观察向量与全局y轴构成的平面内,因此向上向量只用于直接向上或者直接向下的视图中。因此我们需要自己处理一些特殊的情况,或者直接避免它们。对于一些未定义的情形,有时观察者的行为可能会产生无法预期的结果。例如,默认的头部抬起方位意味着如果观察者的兴趣中心固定并且其位置绕着兴趣中心作圆弧运动,那么当观察者正好到达或者离开兴趣中心的上方时,其向上向量会突然转动180°。


目标点
当观察才的位置掠过观察中心时,向上向量将发生翻转
有关观察者的位置和方位,在此还要额外地提一下视场(field of view,FOV)的作用。它完整定义了世界空间中的一个可视范围,其中包括一个可视角度(也可以用半视场角的概念来等价表示,halfangle of view)、近裁剪距离(hither clipping distance)和远裁剪距离(yon clipping distance)。有的时候也用near和 far来代替这里的 hither和 yon。FOV的信息主要用于设置场景的透视投影。
上文中所讨论的观察方式还可以进行一定程度的简化。其他一些观察的方式使用一个附加的向量来指定投影平面的方位,这样就可以在投影平面上定义任意一个不对称于观察方向的视口(从而构建偏移中心的投影方式,以及平行的投影)。可以参考一些图形学标准的文章,从而深入了解这种观察方式的设置手段。
世界空间中的可视范围是通过观察者的位置、观察方向、视场角度、近裁剪平面以及远裁剪平面决定的。
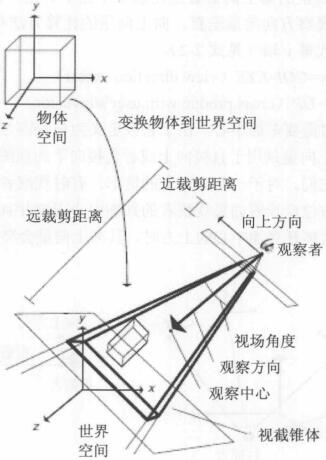
对象到世界空间的变换及世界空间中的视截锥体
这就是视截锥体(view frustum)的定义,即一个包含了所有需要显示的数据的、位于世界空间中的六面体。
为了实现透视投影变换,我们通常需要将对象的数据点集从世界空间变换到眼睛空间(eye space)。在眼睛空间中,观察者位于z轴之上,视线方向与z轴重合。这样我们就可以仅用一个点的z坐标来定义点的深度和透视的远近比例。无论眼睛空间的坐标系统属于左手坐标系还是右手系(不同资料对此的定义不同),观察者的精确位置总是位于z轴之上。本讲中,观察者总是位于坐标原点并朝向左手系的z轴正方向。在眼睛空间〈亦即世界空间)中,视线从观察者的位置上发出,然后分散发射到可见的视截锥体中,后者的形状通常被描述为一个被截短的四棱锥。
透视变换是把对象的数据点从眼睛空间变换到图像空间(image space)。透视变换可以被认为是把观察者的背面视为z轴的负无穷位置,这样所有的视线都可以被认为是互相平行且平行于(眼睛空间的)z轴的。四棱锥形状的视截锥体因而变成了一个矩形的实体,或者说是一个立方体,其中相对的侧面都是互相平行的。因此,在眼睛空间中距离观察者较远的点的x和y坐标会被剧烈缩放,其变化幅度会超过那些距离观察者较近的点。有时我们称之为透视缩短(perspective foreshortening)。在图像空间中,可视范围的x和y坐标通常被标准化为-1到+1之间的值,而z则是从0到1(在有些材料里,z的可见值也会被映射到-1到+1的范围)。然后我们会将图像空间的点缩放和平移(也有可能旋转)到屏幕空间(screen space),即将x和y的可视范围(-1到+1)映射到与窗口或屏幕坐标系统定义的观察区域重合的位置上,但是z坐标不动。各个空间的变换过程如图所示。
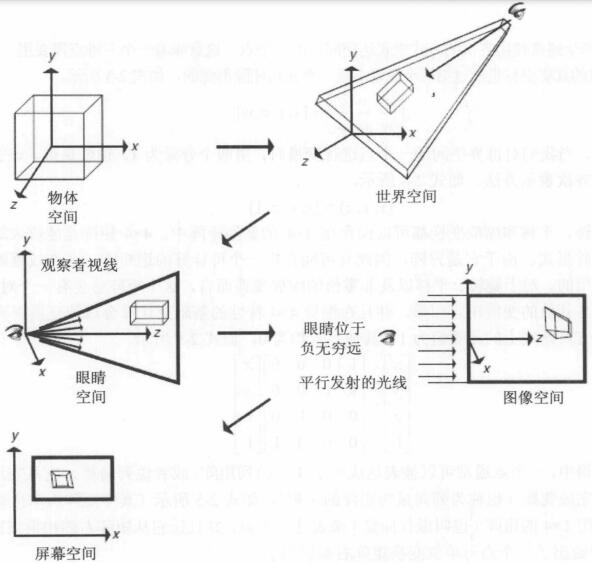
显示流水线中各个空间的变换过程
射线追踪法(ray casting,即不生成后继射线的光线跟踪)与上述方法的变换序列有所区别,因为从观察者位置发射到世界空间的追踪线实质上已经完成了透视变换操作。如果在世界空间中构建这些射线时假设一个虚拟的帧缓存设备(像素坐标)已经放置在观察者面前,那么射线追踪在空间中运算的过程可以简化为如图使用射线追踪进行空间的变换所示的变换操作。因此,我们也可以选择将数据变换到眼睛空间,然后通过虚拟帧缓存在眼睛空间中直接生成射线。
任何情况下,典型的动画制作都是通过下面一种或多种方式完成的:随时修改世界空间中物体的位置和方位、随时修改物体的形状、随时修改物体的显示属性、随时变换物体在世界空间的位置和方位;上述几种变换的集合。

使用射线追踪进行空间的变换
以上就是计算机教程网总结的计算机图形学显示流水线基础知识,更多相关知识请关注计算机教程网公众号( jsjjcwcom)

jsjjcwcom